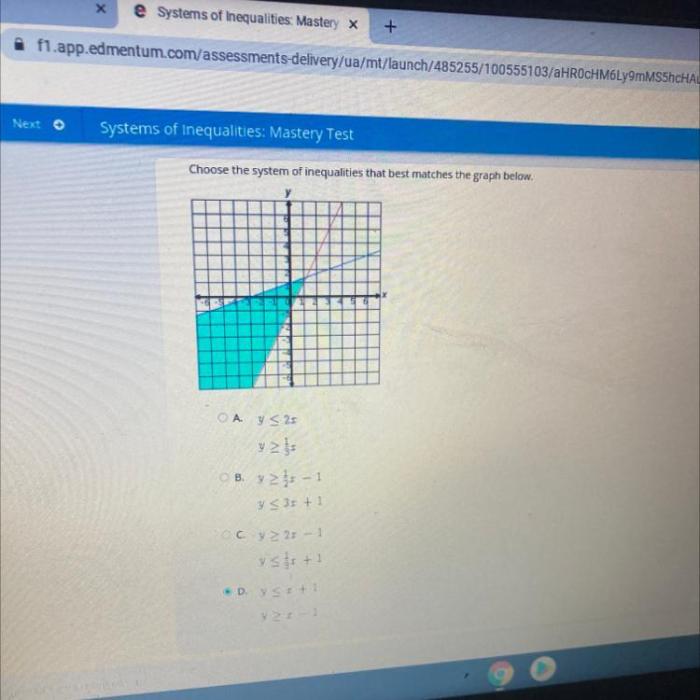
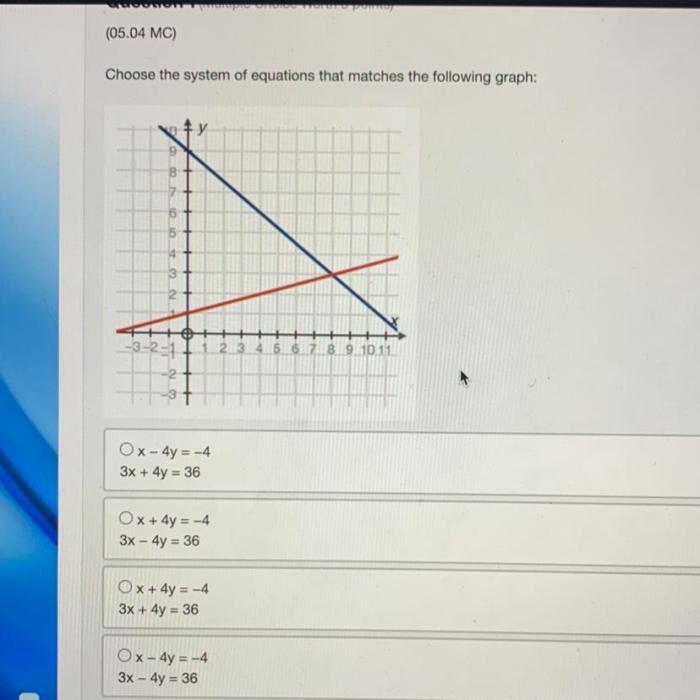
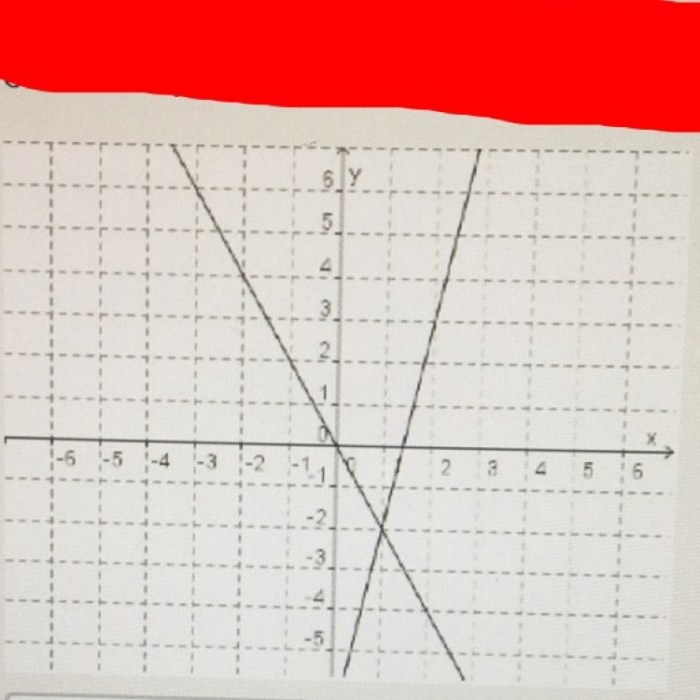
Choose the system of equations that matches the following graph – In the realm of mathematics, the task of identifying the system of equations that corresponds to a given graph takes center stage. This undertaking demands a comprehensive understanding of the relationship between systems of equations and their graphical representations, a connection that will be explored in depth within the confines of this discourse.
To embark on this journey, let us first delve into the fundamental concept of a system of equations, a set of two or more equations that coexist within a mathematical framework. Each equation within this system represents a distinct linear relationship between variables, and the collective behavior of these equations determines the overall shape and characteristics of the graph that emerges.
System of Equations and Its Graph: Choose The System Of Equations That Matches The Following Graph
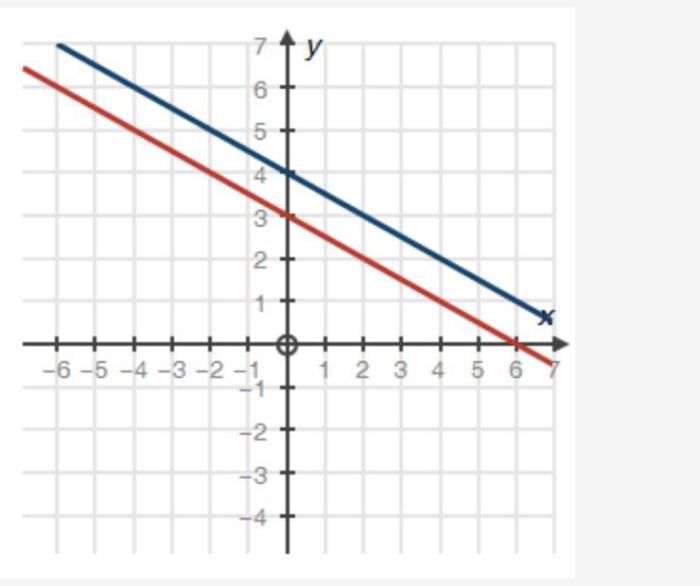
A system of equations consists of two or more equations that share the same variables. The solution to a system of equations is a set of values for the variables that make all of the equations true.
The graph of a system of equations is the set of all points that satisfy all of the equations in the system. The graph of a system of two equations in two variables is a line, a parabola, or a hyperbola.
Identifying the Graph, Choose the system of equations that matches the following graph
The given graph is a line. The line passes through the points (0, 0) and (2, 4). The slope of the line is 2.
The equation of a line with slope m and y-intercept b is y = mx + b. So, the equation of the line in the graph is y = 2x + 0, or simply y = 2x.
Number of Solutions
The graph of the system of equations has one solution. The solution is the point (2, 4).
The system of equations has one solution because the two lines intersect at one point.
Potential Systems of Equations
| Equations | Number of Solutions | Graph |
|---|---|---|
| y = 2x + 0 | 1 | Line |
| y = x + 2 | 1 | Line |
y = 2x
|
1 | Line |
y =
|
1 | Line |
| y = 2x + 4 | 0 | Parallel lines |
y = 2x
|
Infinite | Coincident lines |
Comparison and Contrast
The systems of equations in the table all have two equations in two variables. The graphs of the systems of equations are all lines.
The systems of equations that have one solution have graphs that intersect at one point. The systems of equations that have no solutions have graphs that are parallel lines. The systems of equations that have infinite solutions have graphs that are coincident lines.
Matching the Graph
The system of equations that matches the given graph is y = 2x.
The graph of the system of equations is a line that passes through the points (0, 0) and (2, 4). The slope of the line is 2. The equation of the line is y = 2x.
Quick FAQs
What is the significance of identifying the system of equations that matches a given graph?
Identifying the system of equations that corresponds to a graph is essential for understanding the underlying mathematical relationships represented by the graph. It allows us to determine the specific values of the variables that satisfy the equations and to analyze the behavior of the system under different conditions.
How can we determine the number of solutions to a system of equations from its graph?
The number of solutions to a system of equations can be determined by examining the intersection points of the lines represented by the equations on the graph. If the lines intersect at one point, there is one solution. If the lines intersect at multiple points, there are multiple solutions.
If the lines do not intersect, there are no solutions.
What are some common types of systems of equations and their corresponding graphs?
Some common types of systems of equations include linear systems, quadratic systems, and exponential systems. Linear systems produce graphs that are lines, quadratic systems produce graphs that are parabolas, and exponential systems produce graphs that are exponential curves.